https://www.acmicpc.net/problem/11401
11401번: 이항 계수 3
자연수 \(N\)과 정수 \(K\)가 주어졌을 때 이항 계수 \(\binom{N}{K}\)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
www.acmicpc.net
[문제]
자연수 N과 정수 K가 주어졌을 때 이항 계수 nCk를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
[입력 조건]
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 4,000,000, 0 ≤ K ≤ N)
[코드]
import java.util.*;
public class BaekJoon_11401 {
public static final long p=1000000007;
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
long n=sc.nextInt();
long k=sc.nextInt();
long number=factorial(n); // 분모
long denom=factorial(k)*factorial(n-k)%p; // 분자 (K!*(N-K)!) mod p
// N! * 분모의 역원
System.out.println(number*pow(denom,p-2)%p);
}
// 팩토리얼 구하는 함수
public static long factorial(long n) {
long result=1L;
while(n>1) {
result=(result*n)%p;
n--;
}
return result;
}
/*
* 역원 구하는 함수
* base : 밑, exponent : 지수
*/
public static long pow(long base, long exponent) {
// 지수가 1일 경우 base^1 이므로 base%p를 리턴
if(exponent==1)
return base%p;
// 지수의 절반에 해당하는 base^(exponent/2)를 구한다.
long temp=pow(base,exponent/2);
/*
* 현재 지수가 홀수 였다면
* base^(exponent/2) * base^(exponent/2) * base 이므로
* base를 한 번 더 곱해주어야 한다.
*
* ex) A^9 = A^4 * A^4 * A
*/
if(exponent%2==1)
return (temp*temp%p)*base%p;
return temp*temp%p;
}
}
[알고리즘]
모듈러 연산 기본 성질에서 곱셈의 분배 법칙을 사용해야 한다. 하지만 기존 이항 계수 식에서는 분수로 인해 분배 법칙을 사용할 수 없다. 그러면 이항 계수의 식을 곱셈 꼴로 바꿔야 할 것이다. 나눗셈을 곱셉으로 바꿀 수 있는 방법은 바로 역원을 사용하는 것이다.
이항 계수의 분모에 해당하는 (k!(n-k)!)의 역원을 구해야 한다. 이때 '페르마의 소정리'를 적용해야 한다. 페르마의 소정리의 정의는 다음과 같다.

a ⫮ p 에서 ⫮ 기호는 나눠지지 않는다는 의미이다. 즉, a는 p의 배수가 아니라는 말과 같다. 위 식을 보조정리를 이용하여 바꾸면 아래와 같다.

즉, a (mod p)에 대한 역원은 a^p-2 (mod p) 라는 것이다. 이제 우리가 필요한 분모의 역원을 구해보면 다음과 같다.
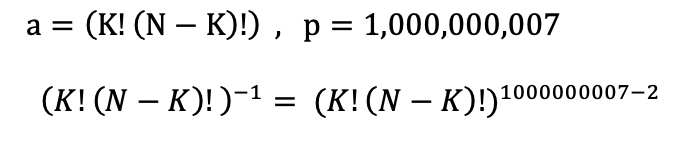
최종적으로 정리해보자.

이와 같이 분모를 역원으로 바꿔 사용하는 방법과 거듭제곱을 분할 정복 방식으로 계산하는 방법을 통해 문제를 해결하면 된다.
[고찰]
이번 문제는 이전 문제를 통해 익혔던 거듭제곱을 분할 정복으로 해결하는 방법 외에도 페르마의 소정리를 이용하여 역원을 구하는 방법까지 알고 있어야 해결할 수 있는 문제였다. 혼자 힘으로는 풀 수 없어 다른 사람들의 풀이를 참고하였다. 수학적 이론과 공식을 사용하여야 풀 수 있는 문제는 아직 많이 약한것 같다. 꾸준히 복습하면서 여태까지 나온 식들을 암기해나가야 겠다.
'백준' 카테고리의 다른 글
| [백준_2805번] 나무 자르기 (0) | 2021.07.09 |
|---|---|
| [백준_1654번] 랜선 자르기 (0) | 2021.07.09 |
| [정수론 및 조합론_11051] 이항 계수 2 (0) | 2021.07.09 |
| [백준_2740번] 행렬 곱셈 (0) | 2021.07.09 |
| [백준_1920번] 수 찾기 (0) | 2021.07.08 |